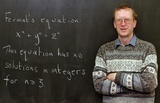
700 тысяч долларов за Великую теорему Ферма!

Именно такую сумму получит британский математик Эндрю Уайлс, который в 1994 году представил доказательство Великой теоремы Ферма. О решении Международного математического союза и Европейского математического общества присудить ему Абелевскую премию, которую иногда называют Нобелевской премией для математиков, объявил президент Норвежской Академии наук и литературы Оле Сейерстед, сообщается на официальном сайте премии.

«Новые идеи, введенные Уайлсом в научный обиход, открыли возможность для последующих прорывов, — сказал глава Абелевского комитета Йон Рогнес. — Немногие математические проблемы имеют такую богатую научную историю и такое эффектное доказательство, как Великая теорема Ферма».

Великий французский математик Пьер Ферма всегда делал свои пометки на полях читаемых математических трактатов и там же формулировал пришедшие на ум задачи и теоремы. Свою Великую теорему, которую иногда называют Последней (Last) он записал с припиской, что найденное им остроумное доказательство этой теоремы слишком длинно, чтобы его можно было поместить на полях книги:

"Наоборот, невозможно разложить куб на два куба, биквадрат на два биквадрата и вообще никакую степень, большую квадрата, на две степени с тем же показателем. Я нашёл этому поистине чудесное доказательство, но поля книги слишком узки для него".

Ферма

Оригинальный текст (лат.)

Cubum autem in duos cubos, aut quadratoquadratum in duos quadratoquadratos & generaliter nullam in infinitum ultra quadratum potestatem in duas eiusdem nominis fas est dividere cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet».

Это было в 1637 году, когда по Франции вовсю скакали мушкетеры, похищали брильянтовые подвески и убивали друг друга на дуэлях.

Что это за теорема и как она сформулирована, насколько сложно ее доказать, лучше всего рассказано в увлекательном фильме замечательного советского режиссера-документалиста Семена Вартбурга.

Попытки доказать ВТФ начались практически сразу же после ее «обнаружения». Над этой задачей бились Эйлер, Дирихле, Лежандр и другие профессиональные математики и дилетанты. Эрнст Куммер попутно создал современную теорию чисел.

Давид Гильберт в своём докладе «Математические проблемы» на II Международном конгрессе математиков (1900) так отозвался о ВТФ:

«Проблема доказательства этой неразрешимости являет разительный пример того, какое побуждающее влияние на науку может оказать специальная и на первый взгляд малозначительная проблема. Ибо, побуждённый задачей Ферма, Куммер пришёл к введению идеальных чисел и к открытию теоремы об однозначном разложении чисел в круговых полях на идеальные простые множители — теоремы, которая теперь, благодаря обобщениям на любую алгебраическую числовую область, полученным Дедекиндом и Кронекером, является центральной в современной теории чисел и значение которой выходит далеко за пределы теории чисел в область алгебры и теории функций».

Именно создание теории чисел можно назвать главным посмертным вкладом Ферма в развитии математики. «Господь создал целые числа, а все остальное - дело рук человека», - так охарактеризовал роль этой теории Леопольд Кронекер. Пифагор считал, что вся Вселенная состоит из целых чисел. Во всяком случае, человек исследует тайны Вселенной пока что чисто цифровыми, дискретными методами.

Эндрю Уайлс, рыцарь-командор Ордена Британской Империи — английский и американский математик, завкафедрой математики Принстонского университета, член научного совета Института математики Клэя, узнал о ВТФ, когда ему было всего десять лет. Вооружившись школьным учебником, он попытался превзойти Эйлера и Дирихле, но, понятно, это ему тогда не удалось.

Он успокоился, хотя как показали дальнейшие события, ненадолго, получил высшее образование и занялся другими проблемами. А конкретно, так называемыми эллиптическими кривыми. Вскоре он познакомился с работами в этой области японцев Симуры и Такаямы, а также француза Вейля. А затем и с доказательством американского математика Кена Рибета, что эти работы напрямую связаны с ВТФ.

Тут «старая любовь» поднялась из глубин подсознания Уайлса и он в течение семи лет пытался добить «Fermat`s last theorem» - так называется ВТФ в его работе, за которую он, собственно говоря, и получил честно заработанные 700 тысяч долларов.

Доказательство было закончено и опубликовано в 1994 году. Вскоре в нем обнаружилась ошибка, но ее с помощью своего помощника Уайлс исправил.

Ферма

Тут на него стали сыпаться всевозможные награды, вплоть до присвоения высокого рыцарского звания.

Поскольку доказательство Уайлса содержит 130 страниц крайне сложного математического текста, от Норвежской Академии наук потребовалось довольно много лет, чтобы убедиться в его корректности.

Но и сейчас с ВТФ и ее доказательством не все так просто и понятно.

Многотысячная армия «ферматистов», то есть фанатов бесконечного, но крайне засасывающего доказательства ее верности или неверности, возмущена и требует продолжения шоу.

А между тем, увлечение доказыванием ВТФ крайне опасно для «романтических вьюношей». Вот что пишет один из возмущенных «ферматистов» на интернет-форуме:

«В математическом сообществе как бы безоговорочно принят факт, что долгожданное доказательство ВТФ действительно найдено. Однако как член математического сообщества, я нахожусь в незадачливом положении для обсуждения или засвидетельствования верности этого доказательство. Мне сказали, что количество времени, необходимое, чтобы получить знания, достаточные для критики доказательство, измеряется годами. После краткого обзора использованного математического аппарата я убедился, что это верно. Поэтому создана неловкая ситуация, кода решение такой классической проблемы предстало в виде, понятном только наиболее искушенным экспертами. Именно по этой причине я пишу эту работу. Надеюсь, что эта работа может служить начальным справочником любому заинтересованному изучением необходимых сведений для собственной проверки верности доказательства ВТФ».

Специально сохраняю стилистику и грамматические ошибки и опечатки оригинала, чтобы показать типичный уровень таких фанатов.

В доказательство Уайлса пытаются вникнуть и более искушенные в математике энтузиасты:

«По-моему, это тот самый случай , когда понять доказательство сложнее, чем обнаружить ошибку. Поэтому я бы поостерегся пока называться Вайлса «великим Вайлсом». - пишет один из них.

«Я, кстати, тоже дочитал до того и что такое "кондукторы", и что такое "модулярные формы", но вот про метод Колывагина-Флаха вообще ничего не понял. А в доказательстве Вайлса это всего лишь начало, отправная точка!» - отвечает ему другой.

Вгрызаются в 130-страничную работу Уайлса и профессионалы:

«Просмотрев эту статью, я снова вижу: доказательство Рибета-Фрея-Уайлса опирается на то, что при разложении дискриминанта кривой Фрея… на простые числа, степень двойки не делится на показатель степени уравнения Ферма, а остальные степени делятся. Если бы в знаменателе не было бы 256, то тогда бы доказательство не годилось. Хорошо бы кто-нибудь это прояснил: почему там 256, и можно ли обобщить Теорему Ферма под доказательство Рибета? Или 256 вообще не причем?».

Ряд скептиков просто отказывают Уайлсу в сколь-нибудь существенном вкладе в эпохальное доказательство:

«Танияма увидел (заметил), сформулировал гипотезу, Вайлс доказывал верность гипотезы. Также ранее вроде было доказательство того, что из верности гипотезы Танияма следует и верность теоремы Ферма. Откуда я делаю вывод, что полученное доказательство - чистая игра формул и случайностей».

Но ближе к истине другие эксперты, которые видят в долгожданном доказательстве ВТФ возможность дальнейших перспективных открытий:

«А вот это, полагаю, не так. Это не случайно, и если нет ошибок, то эта теория отражает какие-то алгебраические свойства трехчленов. Теорема Ферма формулируется для троек чисел, а эллиптические функции, благодаря которым она доказывается, появляются при решении дифференциального уравнения . За этим могут стоять замечательные свойства чисел и единство алгебры. Думаю, что если бы кто смог прояснить эти связи, было бы очень здорово».

И наконец, вывод, под которым я готов, как инженер-математик, подписаться:

«Не могу согласиться с Вашими словами. Чтобы "тупо увидеть" это свойство, надо было потрудиться. Но Вы правы в том смысле, что кажется, здесь все проделано без понимания истинных причин. Думаю, что тот, кто поймет, почему все это так устроено и почему эллиптические функции обладают такими свойствами, и тот, кто сможет это объяснить, сделает больший вклад в математику, чем например, тот же Уайлс. Поэтому искать параллельное доказательство Теоремы Ферма чрезвычайно полезно: если такое будет найдено, то может быть вскроются причины свойств эллиптических функций, а если еще при этом будут придуманы новые методы, то это будет прорыв в математике, возможно лучший за последние 50 лет. Но конечно, нужны новые методы, без них это будет просто объяснение, а не новое открытие».

Итак, Великая теорема Ферма наконец доказана. Но закоренелым «ферматистам» нет причин складывать математическое оружие. Научная общественность жаждет более простого и более общего доказательства.

Возможно и соответствующая премия будет придумана под эту задачу. Ведь, если перефразировать Леопольда Кронекера, Господь лишь придумал целые числа, а грамотно «рассортировать» их - наша задача.

Автор: Владимир Прохватилов, президент Академии реальной политики (Realpolitik), эксперт Академии военных наук

Добавляйте CСб в свои источники дзен